Esta página está dedicada a curiosidades, ilusiones ópticas y textos divertidos, que esperamos sean de tu agrado. En esta ocasión:
¿La cara de un anciano?Luis Monje Arenas
Casi seguro que afirmáis que es un viejo con barba y extraño pelo largo, pero relajad la vista y veréis que, en realidad, es una pareja de novios abrazándose y besándose rodeados de bonitas hojas de parra. Cuesta verlo pero resulta divertido e interesante. Volver al principio de la ilusión Volver al principio
El engaño de la menteSigfrido del Alce Lee rápidamente el texto que aparece dentro del triángulo
Posiblemente leas: "Un pájaro está en el nido solito". Pero existe una errata... ¿La ves? Léelo otra vez con mucho detenimiento, verás que el texto reza: "Un pájaro está en el el nido solito". Inténtalo con tus amigos y verás que, aunque les asegures que no pone lo que creen leer, se empeñarán en no ver el segundo artículo. Volver al principio de la ilusión Volver al principio
|
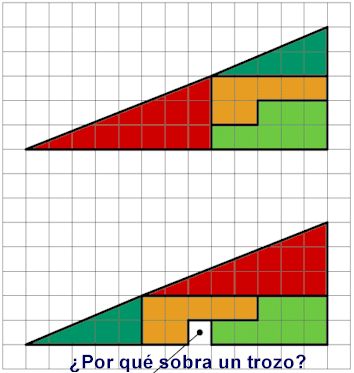 |
Dicho de otra forma: la falsa hipotenusa del supuesto triángulo grande compuesto no es una recta, sino dos que se unen en ese vértice (donde contactan los dos triángulos pequeños).
¿Cómo se comprueba esto sin grandes cálculos?
Observando que las pendientes de las dos hipotenusas pequeñas son distintas entre sí y distintas a la hipotenusa que tendría un triángulo rectángulo de ese tamaño.
En efecto: un triángulo rectángulo de ese tamaño tiene catetos de 5 y 13 cuadritos (diremos c), es decir, que su hipotenusa tendrá una pendiente de 5 c por cada 13 c de longitud base. Entonces, si la hipotenusa del triángulo pequeño tuviese la misma pendiente, con una sencilla regla de tres, tendremos que si a 5 c de altura le corresponden 13 c de longitud, a 2 c de altura le corresponderá: 2 x 13 : 5 = 5,2, es decir, más de los 5 c exactos que aparecen en la figura.
Lo mismo, pero al revés, sucede con el otro triángulo no tan pequeño: 3 x 13 : 5 = 7,8, es decir, menos de los 8 que aparecen en la figura.
Conclusión: la hipotenusa del triangulito más pequeño tiene más pendiente que la del otro no tan pequeño, de manera que al colocarse uno a continuación del otro, la recta unión de ambas hipotenusas no es tal recta, sino dos rectas, es decir, dos lados de un polígono.
En la combinación superior, dicho vértice queda hacia dentro (el ángulo interior de este vértice tiene más de 180º), mientras que en la inferior, queda un ángulo interior de menos de 180º. Obviamente, en la superior, al converger las hipotenusas hacia dentro del polígono, producen una menor superficie. Por eso su superficie es de 32 cuadraditos. En cambio, en la inferior, al converger hacia afuera, producen una mayor superficie, de 33 cuadraditos. En consecuencia, arriba queda todo relleno con las cuatro figuras que suman en conjunto 32 cuadraditos (8+7+5+12), mientras que abajo, sobra un cuadradito al rellenarlo con las 4 figuras, que suman los mismos 32 cuadraditos; porque, evidentemente, las cuatro figuras son siempre idénticas arriba y abajo, lo que es distinto es el conjunto que forman.
Para corroborarlo basta con calcular la superficie del supuesto triángulo rectángulo compuesto. Si tiene catetos de 5 c y 13 c, su superficie será: 5 x 13 : 2 = 32,5 cuadraditos. Es decir, que ni una ni otra combinaciones son triángulos, ya que uno tiene una superficie de 32 y el otro de 33.
Ahí está la respuesta del porqué abajo sobra un trozo.
De hecho, si se miran las figuras de reojo y con desconfianza (como debe observarse todo lo propuesto por Luis Monje), se nota que intenta embaucarnos con una hipotenusa que se hunde un poco (la de arriba) y que se abomba un poco (la de abajo).
Quizás debería haber advertido de la necesidad de tomarse una aspirina antes de leer el presente texto, pero se me olvidó. No sólo Luis hace maldades.
De todas formas, seguro que alguien dará con una solución menos farragosa que ésta y más elegante, pero mis neuronas no dan para más.
Un saludo a todos, y animarse, aunque sea con esas chorradas.
|